Plot

Das Plot-Plugin dient zum Zeichnen von beliebigen Funktionsgraphen:

Parameter-String

• Der Parameter-String enthält alle Funktionen die geplottet werden sollen und Parameter, welche für alle Diagramme definiert werden sollen.
• Funktionen und Parameter sind durch Strichpunkt getrennt.
• Konfigurationsparameter können im Parameter-String oder im PIG-Tag angegeben werden

normaler Funktionsplot (function)

Der Parameter function muss nicht angegeben werden, da er die Standardeinstellung für Plot ist.

mögliche Funktionsdefinitionen:

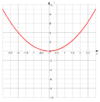
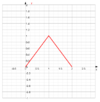
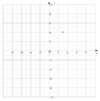
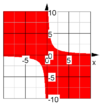
Funktion	Beschreibung	Beispiel	Graph
f(x):= {Funktion in x}	Funktion in einer Variablen	f(x):=x^2
f(t):=[{Funktion x(t)},{Funktion y(t)}]	parametrische Funktion	f(t):=[2*sin(t),2*cos(t)];t:0,2pi
f(x,y):=[[{x1},{y1}],[{x2},{y2}],...]	Linienzug aus Stützpunkten	f(x,y):=[[0,0],[1,1],[2,0]]
f(x,y):=[{x},{y}]	Punkt	f(x,y):=[3,4]
f(x,y):= {boolsche Funktion in x und y}	implizit deklarierte Funktion muss auf der rechten Seite ein boolsches Ergebnis haben!	f(x,y):=x*y<3

Füllungen zwischen Graphen

Füllbereiche können zwischen zwei Funktionen eingefügt werden.

Syntax:

Füllungsdefinition	Beschreibung	Beispiel	Graph
fill:{Funktion1} > {Funktion2}	Füllung des Bereichs wo die Funkion1 größer als die Funktion2 ist	y(x):=-0.1*x^2+7;y(x):=0.2*x+1;fill:ch1>ch2,color=green	:
fill:{Funktion1} < {Funktion2}	Füllung des Bereichs wo die Funkion1 kleine als die Funktion2 ist	y(x):=-0.1*x^2+7;y(x):=0.2*x+1;fill:ch1<ch2,color=green	:
fill:{Funktion1} - {Funktion2}	Füllung des Bereichs zwischen Funkion1 und Funktion2	y(x):=-0.1*x^2+7;y(x):=0.2*x+1;fill:ch1-ch2,color=green	:

• Als Funktionsnamen kann der Name der Funktion, oder die Nummer der Funktion (ch1,ch2,...) verwendet werden
• Nach der Funktionsdefinition kann durch Beistrich getrennt die Füllung konfiguriert werden.

Parameter	Beschreibung	Beispiel
color={Farbe}	Farbe der Füllung setzen	color=blue
size	Linienstärke der Füllungsumrandung	size=5
fill	Füllstärke (mit der Farbe der Linienfarbe) einer Füllung von der Graphenlinie bis zur Nulllinie 0..keine Füllung (Standard) 1..deckend gefüllt	fill=0.3

gespiegelter Funktionsplot (functiony)

X und Y-Achse werden vertauscht!

Beispiel:

f(x):=x^2;x:-3,3;y:-3,3;f:size=5;functiony

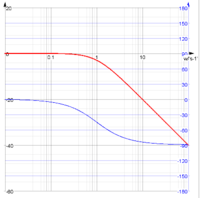
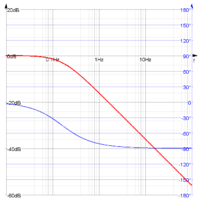
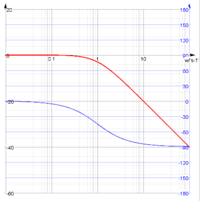
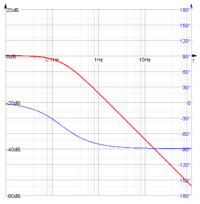
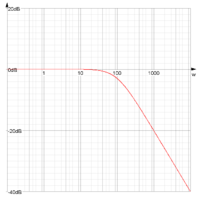
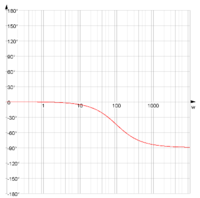
Bodediagramm (bode, bodeabs, bodearg)

Funktion	Beschreibung	Beispiel	Graph
G(s):= {Funktion in s}	Laplace-transformierte	G(s):=1/(1+s);bode;s:0.01,100;abs:-60,20,size=4	:
G(s):= {Funktion in s}	Laplace-transformierte mit Frequenz f	G(s):=1/(1+s);bode;f:0.01,100;abs:-60,20,size=4
G(w):= {Funktion in w}	Fouriertransformierte mit Kreisfrequenz w	G(w):=1/(1+j*w);bode;w:0.01,100;abs:-60,20,size=4	:
G(w):= {Funkion in w}	Fouriertransformierte mit Frequenz f	G(w):=1/(1+j*w);bode;f:0.01,100;abs:-60,20,size=4	:
G(s):= {Funktion in s}	Nur Betragsfrequenzgang	G(s):=1/(1+0.01*s);bodeabs	:
G(s):= {Funktion in s}	Nur Betragsfrequenzgang	G(s):=1/(1+0.01*s);bodearg	:

Konfiguration von Achsen und Funktionen

Alle Konfigurationen zu Achsen und Funktionen beginnen mit dem Namen der Achse oder Funktion gefolgt von einem Doppelpunkt und der durch Beistrich getrennten Parameterliste.

Name:par1=wert1,par2=wert2,switch1,switch2

Name

Name	Beschreibung	Beispiel	Name
Variable	Eine Variable, welche als Parameter einer Funktion auf einer Achse aufgetragen ist	f(x):=x^2+2*x	x
Funktion	Eine Funktion, welche auf einer Achse aufgetragen ist	f(x):=x^2+2*x	f
Absolutbetrag	Der Absolutbetrag einer komplexen Funktion	G(s):=1/(1+s);bode	abs
Argument	Das Argument einer komplexen Funktion	G(s):=1/(1+s);bode	arg

Parameter

Wenn die ersten zwei Parameter aus Variablen und Datensätzen numerisch berechenbar sind, werden sie als Grenzen der Achsen verwendet.

Weitere Parameter:

Parameter	Beschreibung	Beispiel
color	Farbe des Graphen	color=red
size	Linienstärke	size=5
fill	Füllstärke (mit der Farbe der Linienfarbe) einer Füllung von der Graphenlinie bis zur Nulllinie 0..keine Füllung (Standard) 1..deckend gefüllt	fill=0.3
name	Beschriftungstext der Legende	name=abc
eh	Einheit die verwendet werden soll	eh=V

Schalter

Schalter haben keinen Wert, sondern werden nur aktiv wenn sie angegeben werden.

Schalter	Beschreibung
fill	Setzt die Füllstärke auf 0.3 wie wenn fill=0.3 gesetzt ist
name=	löscht die Legendenbeschriftung
1000	setzt die Anzahl der berechneten Werte auf 1000
log	Ändert die Skala der Achse auf eine logarithmische Skala
dB	Ändert die Skala der Achse auf eine dB-Skala

Beispiele

x:-4,5,color=red,size=4
arg:color=blue

allgemeine Parameter

Parameter	Beschreibung	Beispiel
grid=mode	Setzt die Darstellungsart des Hauptgitters! mögliche Modes sind: x,y,all,off	g(x):x+4;g;y:-10,10;grid=off
helpgrid=mode	Setzt die Darstellungsart des Hilfsgitters! mögliche Modes sind: x,y,all,off
axis=mode	Setzt die Darstellungsart der Achsen mögliche Modes sind: x,y,all,off
legend=mode	Setzt die Darstellungsart der Achsenbeschriftung mögliche Modes sind: x,y,all,off
numbers=mode	Setzt die Darstellungsart der Zahlen bei den Achsen mögliche Modes sind: x,y,all,off
w[breite][Auflösung]	Breite und Auflösung des Bildes setzen. Die Breite wird als Zahlenwert zwischen 1 und 100 als Prozentwert angegeben. Als Auflösung kann h für hohe Auflösung, nichts für normale Auflösung, l für verminderte Auflösung und s für minimale Auflösung verwendet werden	w80, w80h, wh, wl, ws, w70h, w90s,w50l
ae achseinheit	Einheit bei den Achslegenden
showparams=off	Schaltet die Anzeige der Parameterwerte einer Parameterfunktion aus (on/off)	f(t):[cos(t),sin(t)];showparams=off
point(f)	Zeichnet die durch Punkte gegebene Funktion nur aus den Stützpunkten	f(x,y):[[0,a],[a,b]];point(f)
line(f)	Zeichnet die durch Punkte gegebene Funktion als Liniezug (Standard)	f(x,y):[[0,a],[a,b]];line(f)
vect(f)	Zeichnet die durch Punkte gegebene Funktion als Vectorkette	f(x,y):[[0,a],[a,b]];vect(f)
ort(f)	Zeichnet die durch Punkte gegebene Funktion aus einzelnen Ortsvektoren	f(x,y):[[0,a],[a,b]];ort(f)
linepoint(f)	Zeichnet die durch Punkte gegebene Funktion als Linienzug mit Stützpunkten	f(x,y):[[0,a],[a,b]];linepoint(f)

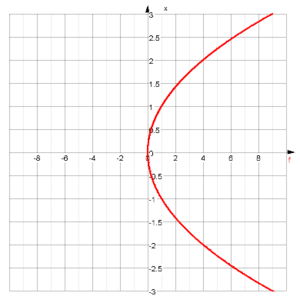
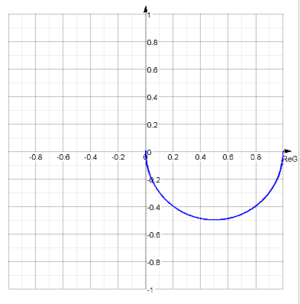
Ortskurve (ortskurve)

Zeichnet die Frequenzgangsortskurve einer Funktion im Laplacebereich mit dem Laplaceoperator s oder einer Fouriertransformierten mit der Kreisfrequenz w.

Beispiel:

G(s):=1/(1+0.01*s);ortskurve;ReG:-1,1;ImG:-1,1;G:size=4,color=blue

siehe auch

• Plugins