Datensätze definieren
Siehe auch Einführung zu Datensätzen
Jede Variable, die im Angabetext in geschwungenen Klammern eingesetzt werden kann, wird über einen Datensatz definiert.
Erstellung aus dem Editor
Wenn im Text der Frage in geschwungenen Klammern Variablenbezeichnungen vorkommen, dann werden beim Verlassen des Editors automatisch die Datensätze angelegt.
Aus dem Variablennamen wird laut SI-Einheitensystem die entsprechende SI-Einheit zugeordnet. Die Wertebereiche und die Einheiten können aber in jeder Kategorie eigens definiert und überschrieben werden.
Erstellung / Änderung über den Datensatz-Bereich
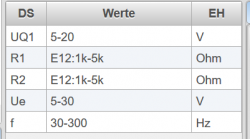
Die Tabelle zur Definition der Datensätze enthält drei Spalten:
- DS: Name der Variable
- Werte: Definition des Wertebereiches und des Types der Variable
- EH: Einheit der Variable
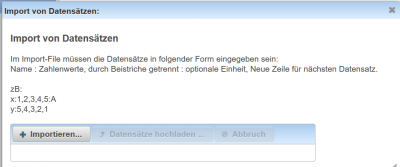
Über das Kontext-Menüs (rechte Maustaste) dieser Datensatz-Tabelle können auch neue Variablen hinzugefügt und bestehende gelöscht werden. Weiters können auch Datensätze mit vordefinierten Werten aus einer Datei importiert werden.
Definition der Werte
Es gibt zwei Varianten einen Wertebereich zu definieren:
- Nur durch die Angabe eines gültigen Bereiches: zB.:1-10,E12:1k-10k
- Durch einen Typbezeichner gefolgt von einem gültigen Bereich: zB.: C:1-10
Folgende Typbezeichner sind möglich:
| Bezeichner | Beschreibung | Beispiel |
| I: | Ganzzahl | I:10-20 |
| V[Dimension]: | Vektor | V3:1-10 |
| M[Zeilen]x[Spalten]: | Matrix der Dimension [Zeilen]x[Spalten] | M3x3:1-10 |
| P[Grad]: | Polynom der Ordnung [Grad] in der Variablen s | P3:1-10 |
| B[Zählergrad],[Nennergrad]: | Polynombruch in der Variablen s mit definiertem Zählergrad und Nennergrad | B2,3:1-20 |
| C: | komplexe Zahl mit zufälligem Winkel zwischen 0° und 360° | C:1-10 |
| komplexe Zahl mit Betrag und Winkel in Grad | C:1-10arg10-90 | |
| komplexe Zahl mit Realteil und Imaginärteil | C:1-10j1-10 | |
| F[ziffern]: | Gleitkommazahl mit einer definierten Anzahl gültiger Ziffern | F3:5-9 |
| S: | Zeichenketten durch Beistrich getrennt | S:rot,grün,blau |
| R: | Regulärer Ausdruck: Erzeugt einen String auf den der reguläre Ausdruck trifft. | R:[a-m]x?[^B]+ |
| R[stellen]: | Regulärer Ausdruck erzeugt einen String mit "stellen" Zeichen | R5:.+ |
| R[minstellen]-[maxstellen]: | Regulärer Ausdruck mit einen Stellenanzahl von "minstellen" bist "maxstellen" | R5-8:[a-z]+\d+ |
| sI:wert,wert,wert | erzeugt Ganzzahl-Datensätze aus den angegebenen Werten, wobei die Reihenfolge der Werte wie angegeben beibehalten wird! (Zahlenbereiche sind hier nicht erlaubt!!) | sI:5,78,2,-5,4 |
| sF:wert,wert,wert | erzeugt Gleitkomma-Datensätze aus den angegebenen Werten, wobei die Reihenfolge der Werte wie angegeben beibehalten wird! (Zahlenbereiche sind hier nicht erlaubt!!) | sF:34.5,3.4,6,5,-43.4 |
Bereichsdefinitionen
Folgende Bereichsdefinitionen sind möglich:
| Beschreibung | Beispiel |
| Zahl | 45 |
| Zahl mit Einheitenvielfachen | 15k |
| mehrere Zahlen, durch Beistrich getrennt | 34,15k,24.4m |
| Zahlenbereich mittels Bindestrich | 3-15 |
| Ganzzahl-Bereiche | I3-15 |
| Eine bestimmte Anzahl von Werten aus einem Zahlenbereich | 13:45-130 |
| Normreihe | E12:10k-80k |
| Dezimale Reihe | D3:10-300 |
Mögliche Normreihen mit logarithmisch verteilten Werten pro Dekade: E3,E6,E12,E24,E48
Mögliche dezimale Reihen mit gleicheverteilten Werten pro Dekade: D2, D4, D10, D20, D40
Mögliche Einheitenvielfache: m,u,n,p,f,a,k,M,G,T
Einheiten
- Als Einheit kann jede gültige SI Einheit angegeben werden
- Beginnt die Einheit mit einem Gleichheitszeichen, so wird die Einheit bei der Darstellung der Variable in der angegebenen Form und mit dem angegebenen Prefix erzwungen.
- Als Sondereinheiten sind zulässig
| dB | Dezibel |
| % | Prozent |
| ppm | parts per million |
| ° | Grad |
| € | Euro |
| $ | Dollar |
- Bei komplexen Zahlen kann durch Beistrich getrennt die Darstellung der komplexen Zahl definiert werden. Folgende Darstellungsvarianten sind zulässig:
| karti | karthesische Darstellung mit "i" als komplexen Operator (1+2i) |
| kartj | karthesische Darstellung mit "j" als komplexen Operator (1+2j) |
| poldeg | Polarkoordinaten Darstellung in Grad 2arg30° |
| polrad | Polarkoordinaten Darstellung in Radianten 2arg0.2 |
| polideg | Exponentialdarstellung mit "i" als komplexen Operator und Winkel in Grad 1*e^20°i |
| poljrad | Exponentialdarstellung mit "i" als komplexen Operator und Winkel in Radiant 1*e^0.2i |
| poljdeg | Exponentialdarstellung mit "i" als komplexen Operator und Winkel in Grad 1*e^20°j |
| poljrad | Exponentialdarstellung mit "i" als komplexen Operator und Winkel in Radiant 1*e^0.2j |