ZielEinheit

Die Zieleinheit von Berechnungsfragen und Mehrfachberechnungsfragen definiert die Einheit und die Art der Verarbeitung des Ergebnisses, welches der Schüler eingeben soll.

Neben der Einheit die der Schüler eingeben soll/muss kann auch die Art der symbolischen Verarbeitung und ein Muster wie die Lösung aussehen soll definiert werden.

Die Zieleinheit ist eine Zeichenkette mit einem definierten Syntax, da das Eingabefeld der Zieleinheit für komplexere Angaben zu klein ist und der Syntax nicht immer bekannt ist kann die Zieleinheit auch über einen Dialog eingegeben werden, welcher über Doppelklick auf die Zieleinheit erreicht wird.

Dialog zur Definition der Zieleinheit

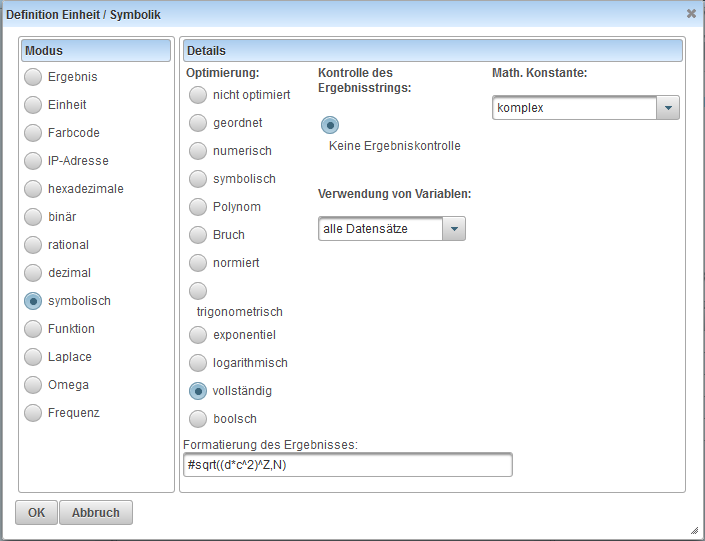
Durch einen Doppelklick auf die Zieleinheit erhält man der Dialog zur Definition der Zieleinheit.

In diesem Dialog wird die Zieleinheit konfiguriert und es wird eine zugehörige Zeichenkette für die Zieleinheit erzeugt.

Im linken Teil des Dialogs wird die Art der Zieleinheit eingstellt (Für genauere Erklärung siehe unten bei Syntax der Zieleinheit-Zeichenkette).

Bei Formatierung der Zeichenkette kann ein Muster definiert werden, welches der Ausdruck des Schülers erfüllen muss. Mehrere Muster welche durch Raute getrennt werden können angegeben werden, wobei der Schülerausdruck mindestens einem Muster entsprechen muss.

Syntax der Zieleinheit-Zeichenkette

Die Zieleinheit beginnt mit einem optinalen Gleichheitszeichen gefolgt von Einheit, Funktion oder symbolischer Berechnungsart. Danach werden alle gültigen Suchmuster durch Raute getrennt angehängt

keine Zieleinheit

Ist keine Zieleinheit angegeben, so muss der Schüler als Ergebnis ein Ergebnis angeben welches die gleiche Dimension und den gleichen Datentyp wie das Ergebnis der Berechnung hat.

Der Schüler kann hierbei auch IP-Adressen(getrennt durch Punkte), Hexadezimalzahlen(beginnen mit 0x) oder Binärzahlen(beginnen mit 0b eingeben, welche für den Ergebnisvergleich in eine Ganzzahl umgewandelt werden.

Einheiten des SI-Systems

• Beginnt die Zieleinheit mit einem Gleichheitszeichen, so muss der Schüler die Einheit, welche rechts neben dem Gleichheitszeichen steht genauso eingeben wie angegeben.

=VA

• Beginnt die Einheit mit einem Fragezeichen, so muss der Schüler die angegebene Einheit verwenden, darf jedoch einen gültigen Einheitenvielfachen-Vorsatz vor dieser Einheit verwenden. (zB.: statt m/s darf der Schüler auch km/s oder m/ms verwenden, er darf jedoch nicht m/h verwenden da die Stunde kein Einheitenvorsatz für die Sekunde ist).

?km/h

• Beginnt die Zieleinheit mit einer gültigen Einheit ohne Gleichheitszeichen oder Fragezeichen, so muss der Schüler eine Einheit der gleichen Dimension verwenden. Diese Angabe dient einerseits zur Kontrolle ob die Lösung des Lehrers auch die selbe Dimension hat, andererseits wird dem Schüler nach der Abgabe die richtige Lösung der Berechnung in dieser Einheit angezeigt.

m/s

• an die Einheit kann noch eine Ganzzahl welche die Anzahl der gültigen Ziffern angibt durch einen Beistrich getrennt angehängt werden. Diese Ziffernanzahl wird für die Anzeige der richtigen Lösung verwendet hat jedoch keinen Einfluss auf die Bewertung!

(zB: A,2 bedeutet Einheit Ampere mit 2 gültigen Ziffern in der Ergebnis-Anzeige)

• Für komplexe Zahlen kann an die Einheit noch die Art der Darstellung der komplexen Zahl durch einen Beistrich getrennt eingestellt werden. Das Ergebnis muss dann in dieser Form eingegeben werden!!

Art	Darstellung	Eingabe
pol	Polarform	1arg0.15 1arg22° 1arg(22°) 1arg(0.15) 1*e^0.15i 1*e^i0.15 1*e^(0.15i) 1*e^(i0.15) 1*e^(0.15*i) 1*e^(i*0.15) 1*e^0.15j 1*e^j0.15 1*e^(0.15j) 1*e^(j0.15) 1*e^(0.15*j) 1*e^(j*0.15)
poli	Polarform in i	1*e^0.15i 1*e^i0.15 1*e^(0.15i) 1*e^(i0.15) 1*e^(0.15*i) 1*e^(i*0.15)
polj	Polarform in j	1*e^0.15j 1*e^j0.15 1*e^(0.15j) 1*e^(j0.15) 1*e^(0.15*j) 1*e^(j*0.15)
polrad	Polarform Radiant	1arg(0.15) 1*e^0.15i 1*e^i0.15 1*e^(0.15i) 1*e^(i0.15) 1*e^(0.15*i) 1*e^(i*0.15) 1*e^0.15j 1*e^j0.15 1*e^(0.15j) 1*e^(j0.15) 1*e^(0.15*j) 1*e^(j*0.15)
poldeg	1arg22° 1arg(22°)
kart	karthesische Koordinaten	2+3i 2+3*i 2+i*3 2+i3 i3+2 i*3+2 3i+2 3*i+2 2+3j 2+3*j 2+j*3 2+j3 j3+2 j*3+2 3j+2 3*j+2
karti	karthesische Koordinaten 2+2i	2+3i 2+3*i 2+i*3 2+i3 i3+2 i*3+2 3i+2 3*i+2
kartj	karthesische Koordinaten 2+2j	2+3j 2+3*j 2+j*3 2+j3 j3+2 j*3+2 3j+2 3*j+2

• Beispiele:

Zieleinheit	berechnetes Ergebnis	korrektes Ergebnis	Ergebnis mit Einheitenfehler	Falsches Ergebnis
	2m/s	2m/s oder 0.002km/s oder 7.2km/h	2m	2km oder 7.2km
m/s	2m/s	2m/s oder 0.002km/s	2m oder 7.2km/h	2km oder 7.2km
=m/s	2m/s	2m/s		2km oder 7.2km oder 7.2km/h 0.002km/s
kart	3+6*%i	3+6i 3+6*j		6.7082arg63.435°

Sondereinheiten für ganze Zahlen

Sondereinheiten für ganze Zahlen verhalten sich immer wie mit vorangestelltem Gleichheitszeichen, weshalb das vorangestellt Gleichheitszeichen auch weggelassen werden kann. Das bedeutet der Schüler muss das Ergebnis immer in der Form eingeben wie es die Zieleinheit verlangt!

Sondereinheit	Bedeutung	Zieleinheit	korrekte Antwort	falsche Antwort
color	Widerstandsfarbcode ohne Toleranz mit 3 Ringen. Hierbei wird nur der Zahlenwert des Ergebnisses verglichen, der Schüler braucht/darf keine SI-Einheit zusätzlich angeben. Als Farbcode	color oder =color	rot-rot-orange	rot-blau-orange oder 22kOhm
ip	IP-Adresse IPv4 in der auch binäre und hexadezimale Zahlen erlaubt sind	ip oder =ip	10.32.1.7 oder 10.0x20,1,0b111	169869575
hex	Hexadezimalzahl	hex oder =hex	0x20 oder 20	32
bin	Binärzahl	bin oder =bin	0b101 oder 101	5
long	Dezimale Ganzzahl	long oder =long	32	30 oder 0x20 oder 0b100000

rational (Brüche)

Bei der Zieleinheit rational muss der Schüler einen Bruch aus Ganzzahlen eingeben.

rational unterstützt keine Einheiten!

Bei =rational muss der Schüler exakt den gleichen Bruch wie gefordert eingeben, ohne Gleichheitszeichen darf der Schüler jeden Bruch eingeben der den gleichen Wert wie gefordert darstellt (auch ungekürzt).

symbolische Berechnungen

Syntax: Optimierungsgrad;Konstantenverarbeitung;Datensatzverarbeitung#Muster1#Muster2

Soll der Schüler ein symbolisches Ergebnis eingeben, so muss die symbolische Berechnung gewählt werden. Je nach Optimierungsgrad gibt es verschiedenen symbolische Berechnungsmodie, welche im Dialog nach der Auswahl der symbolischen Berechnung in der zweiten Spalte des Dialogs ausgewählt werden können.

Optimierungsgrad

Der Optimierungsgrad gibt an, wie das Schülerergebnis und die Lösung des Beispiels umgeformt werden dürfen um dann den gleichen Ausdruck zu liefern.

Folgende smbolischen Modi sind definiert:

Zieleinheit	Optimierungsgrad	Beschreibung
symbolnone	Nicht optimiert	Der Schüler muss den Ausdruck exakt gleich wie im Ergebnis eingeben
symbolorder	Reihenfolge optimiert	Der Schüler darf bei den Grundrechnungsarten die Reihenfolge der Operanden vertauschen
symbolnumeric	numerische Berechnungen werden ausgewertet	Der Schüler darf statt 2 auch 1+1 oder 4/2 etc. schreiben, da alle numerischen Berechnungen ausgewertet werden
symbolic	symbolische Auswertung	symbolische Berechnungen der Grundrechnungsarten werden ausgewertet, Brüche werden gekürzt
symbolpolynom	Polynome ausmultiplizieren	Produkte von Summen werden ausmultipliziert wenn sie als Term in einer weiteren Summen vorkommen
symbolbruch	gemeinsame Nenner bilden	gemeinsamer Nenner von Brüchen wird bestimmt und ausmultipliziert
symbolnormbruch	Polynombrüche Normieren	Polynombruchfunktionen werden auf 1 für den Zahlenwert der Summenelemente normiert (noch nicht realisiert)
symboltrig	trigonometrische Optimierung	Trigonometrische Funktionen werden vereinfacht (noch nicht realisiert)
symbolexp	Optimierung von Exponentialfunktionen	Exponentialfunktions-Terme werden vereinfacht (noch nicht realisiert)
symbollog	Optimierung von logarithmischen Funktionen	Logarithmus-Therme werden vereinfacht (noch nicht realisiert)
symbolfull	vollständige Optimierung	Alle Optimierungstufen werden ausgeführt bzw. wenn das nicht hilft wird das Ergebnis durch Testvektoren numerische geprüft.
symbolboolsch	Optimierung von boolschen Funktionen	boolsche Funktionen werden vereinfacht (noch nicht realisiert)

Nach dem Optimierungsmode folgt durch Strichpunkt getrennt die Verarbeitungsart von Konstanten und durch einen weiteren Strichpunkt getrennt die Verarbeitungsart von Datensätzen.

Konstantenverarbeitung

Hier wird definiert welche Konstanten bei der Berechnung der Lösung als Zahlenwert eingesetzt werden.

Die Konstantenverarbeitung bezieht sich hierbei nur auf Konstante welche nicht mit einem Prozent beginnen! Alle Konstanten welche mit einem Prozent beginnen bleiben solange erhalten, bis sie numerisch ausgewertet werden, dann werden sie immer sofort eingesetzt!

Folgende Möglichkeiten gibt es für die Konstantenverarbeitung:

Beschreibung
	Ist kein String angegeben, so wird wie constscomplex verarbeitet
constsmath	Es werden die mathematische Konstanten i,j,e und pi im Ergebnis eingesetzt
constscomplex	Es wird nur der komplexe Parameter i,j im Ergebnis eingesetzt (Standard)
constsnone	Es werden keine Konstanten im Ergebnis eingesetzt
consts(e)	Es wird nur die Konstante e im Ergebnis eingesetzt
constsall	Es werden alle definierten Konstaten im Ergebnis eingesetzt

Datensatzverarbeitung

Hier wird definiert welche Datensätze bei der Berechnung der Lösung als Zahlenwert eingesetzt werden. Wird ein Datensatz nicht eingesetzt, so wird er in einem symbolischen Ergebnis wie eine Variable behandelt.

Folgende Möglichkeiten gibt es für die Konstantenverarbeitung:

Beschreibung
	Ist kein String angegeben, so wird wie constvarsall verarbeitet
constvars(u,i)	Es werden nur die Datensätze von u und i als Zahlenwert eingesetzt
constvarsnone	Es wird kein einziger Datensatz in das Ergebnis eingesetzt
constvarsall	Es werden alle Datensätze in das Ergebnis eingesetzt (Standard)

Funktionen

Funktionen sind spezielle symbolische Ausdrücke, bei denen nur definiert Funktionsparameter als Variable vorkommen dürfen. Da diese Variablen durch Name und Einheit vorgegeben sind, ist auch eine Einheitenprüfung von Funktionen mögliche, was bei symbolischen Ausdrücken im Allgemeinen nicht möglich ist.

Muster

Das Muster dient vor allem bei symbolischen Auswertungen dazu, um zu definieren, wie die Lösung aussehen kann. Ist ein Muster definiert, so wird automatische mit Symbolfull ausgewertet. Hierbei wird zuerste überprüft, ob die Schülereingabe dem Suchmuster entspricht, und danach noch geprüft ob der Ausdruck des Schülers die gleiche Funktion ergibt wie der Ausdruck im Ergebnis.

Mehrere Muster welche durch Raute getrennt werden können angegeben werden, wobei der Schülerausdruck mindestens einem Muster entsprechen muss.

Im wesentlichen gibt es zwei Arten wie das Suchmuster definiert sein kann:

• Als Mengendefinition wenn das Suchmuster mit einer eckigen Klammer beginnt
• ansonsten als regulärer Ausdruck, der vom Syntax her an die regulären Ausdrücke von Java angelehnt ist sich jedoch bei der Klammerung und den Platzhaltern von den Java-RegExp unterscheidet.

Zeichen für die Definition

Folgende Zeichen sind definiert:

Zeichen	Bedeutung
N	Natürliche Zahl
Z	ganze Zahl
R	reelle Zahl
C	komplexe Zahl
G	reelle Zahl in Exponentialschreibweise zB:1.0e24
V	beliebige Variable welche mit einem Buchstaben beginnt und aus Buchstaben und Zahlen besteht
K	Konstante
E	Einheit

Alle anderen Zeichen haben keine spezielle Funktion.

Mengendefinition

Bei der Mengendefinition werden zu Beginn in eckigen Klammern alle Elemente definiert welche im Ergebnis vorkommen dürfen gefolgt von allen Funktionen durch Beistrich getrennt.

Beispiele:

Muster	trifft bei	trifft nicht bei
[NK*(],sin,cos	4 pi 2*pi sin(2*pi) sin(4) 5*sin(4)	tan(pi) sin(pi/2) 5+sin(4)
[N*]	3*4 3	3+4 1.2*3

Definition als regulärer Ausdruck

Ein Regulärer Ausdruck besteht aus den definierten Mengen, fixen Zeichen und Gruppierungen mit Verknüpfungen.

Die Mengen NZRCGVKE sind wie schon zuvor definiert.

Für Gruppierung und Verknüpfung stehen folgende Zeichen zur Verfügung:

Zeichen	Bedeutung
{ }	Gruppierungsklammer
&	logische Und-Verknüpfung des linken und rechten Ausdrucks
|	logische Oder-Verknüpfung des linken und rechten Ausdrucks
?	optionales Vorkommen eines Zeichens (Das Zeichen links von ? kann Vorkommen, oder auch nicht)
{ }?	optionales Vorkommen einer Gruppe
{ }+?	Gruppe kann einmal oder mehrmals vorkommen
{ }*?	Gruppe kann nicht, einmal oder mehrmals vorkommen

Beispiele:

Muster	passende Lösungen	nicht passende Lösungen
cd	ab cd	ac
R}{*|+|-|/}?}+?	3+2.4*3.54+3/6*2