ZielEinheit

Die Zieleinheit von Berechnungsfragen und Mehrfachberechnungsfragen definiert die Einheit und die Art der Verarbeitung des Ergebnisses, welches der Schüler eingeben soll.

Neben der Einheit die der Schüler eingeben soll/muss kann auch die Art der symbolischen Verarbeitung und ein Muster wie die Lösung aussehen soll definiert werden.

Die Zieleinheit ist eine Zeichenkette mit einem definierten Syntax, da das Eingabefeld der Zieleinheit für komplexere Angaben zu klein ist und der Syntax nicht immer bekannt ist kann die Zieleinheit auch über einen Dialog eingegeben werden, welcher über Doppelklick auf die Zieleinheit erreicht wird.

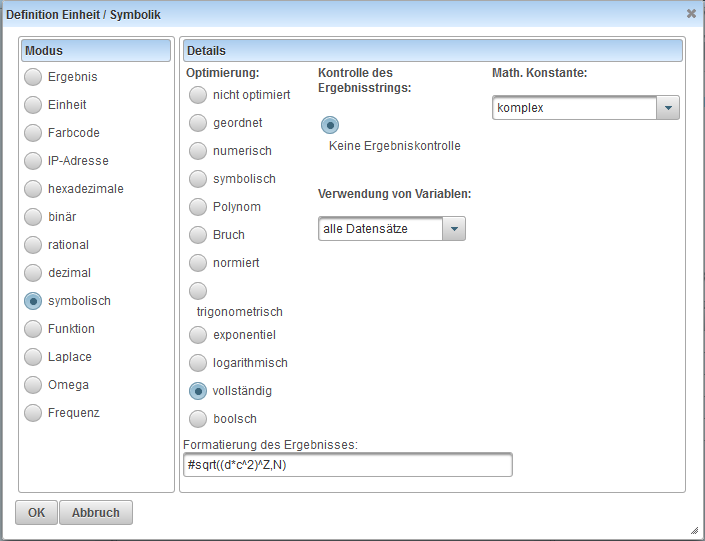
Dialog zur Definition der Zieleinheit

Durch einen Doppelklick auf die Zieleinheit erhält man der Dialog zur Definition der Zieleinheit.

In diesem Dialog wird die Zieleinheit

Syntax der Zieleinheit-Zeichenkette

keine Zieleinheit

Ist keine Zieleinheit angegeben, so muss der Schüler als Ergebnis ein Ergebnis angeben welches die gleiche Dimension und den gleichen Datentyp wie das Ergebnis der Berechnung hat.

Einheiten des SI-Systems

• Beginnt die Zieleinheit mit einem Gleichheitszeichen, so muss der Schüler die Einheit, welche rechts neben dem Gleichheitszeichen steht genauso eingeben wie angegeben.
• Beginnt die Zieleinheit mit einer gültigen Einheit ohne Gleichheitszeichen, so muss der Schüler die angegebene Einheit verwenden, darf jedoch einen gültigen Einheitenvielfachen-Vorsatz vor dieser Einheit verwenden. (zB.: statt m/s darf der Schüler auch km/s oder m/ms verwenden, er darf jedoch nicht m/h verwenden da die Stunde kein Einheitenvorsatz für die Sekunde ist).

Sondereinheiten

Beginnt eine Sondereinheit mit einem Gleichheitszeichen, so muss der Schüler den Wert in der Sondereinheit angeben. Fehlt das Gleichheitszeichen, so darf der Schüler auch andere gültige Darstellungsarten des Ergebnisses verwenden.

Sondereinheit	Bedeutung	Beispiel	korrekte Antwort	falsche Antwort
color	Widerstandsfarbcode ohne Toleranz mit 3 Ringen. Hierbei wird nur der Zahlenwert des Ergebnisses verglichen, der Schüler braucht/darf keine SI-Einheit zusätzlich angeben. Als Farbcode	color =color	rot-rot-orange, 22kOhm rot-rot-orange	rot-blau-orange 22kOhm
ip	IP-Adresse IPv4 in der auch binäre und hexadezimale Zahlen erlaubt sind	ip =ip	10.32.1.7 oder 10.0x20,1,0b111 oder 169869575 10.32.1.7 oder 10.0x20,1,0b111	169869575
hex	Hexadezimalzahl	hex =hex	0x20 oder 32 0x20 oder 20	20 32

• ip
• hex
• bin