Berechnungen: Unterschied zwischen den Versionen
| Zeile 703: | Zeile 703: | ||
| pvforeachline || Führt für jedes Punktepaar einer Punktemenge eine Berechnung aus und verbindet die Ergebnisse mit der Aggregatfunktion || pvforeachline([[2,3],[4,5],[6,3],[-2,4]],p,pvlineabs(p),"+") || 10.890684873 || 6075 | | pvforeachline || Führt für jedes Punktepaar einer Punktemenge eine Berechnung aus und verbindet die Ergebnisse mit der Aggregatfunktion || pvforeachline([[2,3],[4,5],[6,3],[-2,4]],p,pvlineabs(p),"+") || 10.890684873 || 6075 | ||
|- | |- | ||
| loop || Führt eine Zählschleife aus loop(Variable,Startwert,Wiederholbedingung,Inkrement,Ausdruck,Aggregatsfunktion). <br>Ohne Aggregatsfunktion wird ein Feld mit den Ergebnissen der Schleifeniterationen geliefert. || loop(i,1,i<7,i++,i,"+") | | loop || Führt eine Zählschleife aus loop(Variable,Startwert,Wiederholbedingung,Inkrement,Ausdruck,Aggregatsfunktion). <br>Ohne Aggregatsfunktion wird ein Feld mit den Ergebnissen der Schleifeniterationen geliefert. || loop(i,1,i<7,i++,i,"+")<br>loop(i,1,i<7,i:i+2,i) || 21<br>[1,3,5] || 6077 | ||
|- | |- | ||
|} | |} | ||
Version vom 28. Oktober 2021, 09:49 Uhr
Allgemeines
Berechnungen werden in mehreren Bereichen der Frageerstellung verwendet und bilden die Basis für Berechnungsfrage und Mehrfachberechnungsfrage.
Alle Berechnungen unterstützen Einheiten und symbolische Auswertung.
Grundsätzlicher Aufbau der Ergebnis-Berechnung bei Fragen mit Berechnungen
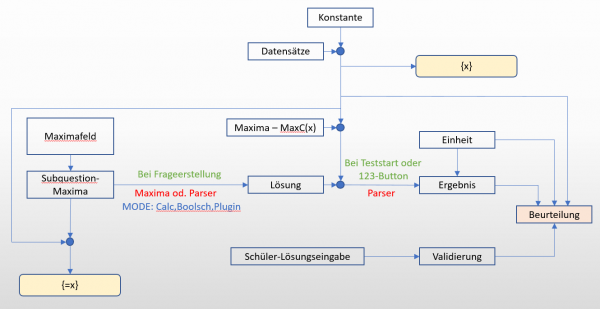
Die Berechnung und die Beurteilung einer Frage teilt sich in 3 grundsätzliche Schritte:
- Berechnnug der geschlossenen Lösung (Formel) aus den Maxima-Feldern
- Berechnung des Ergebnisses einer Frage durch Einsetzen der Zahlenwerte aus den Datensätzen in die geschlossene Lösung
- Beurteilung der Schülereingabe durch Vergleich mit dem Ergebnis
Konstante
Alle Konstante welche in Letto definiert sind beginnen mit einem Prozentzeichen. Verwendet man den Variablennamen ohne Prozenzzeichen, so wird die Konstante wie eine Variable mit dem Wert der Konstanten verwendet.
Liste der definierten Konstanten:
| Name | Wert | Beschreibung |
| %i | i | komplexer Parameter als Lösung der Gleichung x^2=-1 |
| %j | i | komplexer Parameter als Lösung der Gleichung x^2=-1 Wichtig: Wir nur vom Parser unterstützt, nicht von Maxima |
| %e | 2.718281828459045 | Eulersche Zahl |
| %pi | 3.141592653589793 | Kreiszahl |
| %mu0 | magnetische Feldkonstante | 4*%pi*1E-7'Vs/Am' |
| %m0 | magnetische Feldkonstante (alt, wird bald entfernt werden) | 4*%pi*1E-7'Vs/Am' |
| %epsilon0 | elektrische Feldkonstante | 8.85418781762039E-12'As/Vm' |
| %e0 | elektrische Feldkonstante (alt, wird bald entfernt werden) | 8.85418781762039E-12'As/Vm' |
| %c0 | Lichtgeschwindigkeit | 299792458'm/s' |
| %Qe | Elementarladung | 1.602176620898E-19As |
| %g | Erdbeschleunigung | 9.81'm/s^2' |
| %NA | Avogadro Konstante | 6.02214085774E23/mol |
| %k | Stefan Bolzman Konstante | 1.3806485279E-23'J/K' |
| %R0 | Universelle Gaskonstante | 8.314459848'J/Kmol' |
| %h | planksches Wirkungsquantum | 6.6260704081E-34Js |
Berechnung mit Maxima
- Maxima wird nur für symbolische Berechnungen bei der Erstellung von Beispielen verwendet. Hierbei wird, wie schon oberhalb im Schema angegeben, zuerst die Moodle.mac geladen, dann das Maxima-Feld berechnet und anschließend die Maxima-Felder aller Teilfragen. Das Ergebnis der Berechnung wird dann als symbolischer Ausdruck im Lösungfeld eingetragen.
- Da zum Zeitpunkt der Maxima-Berechnung keine Datensätze vorhanden sind, kann keine numerische Berechnung in Maxima durchgeführt werden, welche die Datensätze benötigt. Dies muss der interne Parser zum Zeitpunkt des Online-Test-Laufes erledigen. Numerische Berechnungen, welche der interne Parser nicht kann können deshalb auch nicht mit Maxima berechnet werden.
- Da das Lösungsfeld, welches mit Maxima berechnet wird symbolisch ausgewertet wird, können in Maxima sämtliche symbolischen Berechnungsverfahren angewendet werden, welche ein symbolisches Ergebnis liefern und keine numerischen Werte der Datensätze benötigen.
- Reicht im Maximafeld die Zeilenlänge nicht aus ist es möglich einen defninierten Zeilenumbruch zu realisieren. Schreiben Sie dazu "\" (einfacher Backslash) am Ende der Zeile.
- Funktionsdeklarationen wie f(x):=x^2 mit Doppelpunkt-Ist-Gleich sind im Maxima-Feld nur eingeschränkt bis gar nicht verwendbar, da sie vom Parser nicht unterstützt werden.
- Mengen von Maxima sind in LeTTo nicht verwendbar. LeTTo verwender hierzu eigene Funktionen des Parsers welche mit "set" beginnen und auf Vektoren basieren.
Berechnung mit dem internen Parser
- Der interne Parser kann durch Wahl der Checkbox "Parser" anstatt von Maxima für die Berechnung des Maxima-Feldes verwendet werden.
- Jedenfalls wird der Parser zur Test-Laufzeit für die Berechnung des Ergebnisses einer Frage aus Lösung und Datensätzen und zum Berechnen der Schülereingabe verwendet.
Operatoren
VORSICHT mit MAXIMA
- Einige Operatoren sind in Maxima anders, oder nicht definiert. Möchte man im Maximafeld die Operatoren des Parsers-verwenden, so muss das gesamte Maxima-Feld mit dem Parser gerechnet werden. Man verliert dadurch jedoch die Vorteile der Maxima-Berechnung.
- Alternativ kann man statt der Operatoren auch Funktionen verwenden (zB: ne() statt != ). Diese werden dann von Maxima zwar nicht ausgewertet, die Berechnung bleibt aber trotzdem korrekt und kann mit Maxima durchgeführt werden.
- Es gibt einige Funktionen welche in Maxima existieren aber im Parser nicht, oder mit anderem Syntax.
- Wenn diese von Maxima nicht ausgewertet werden können, da sie Datensätze enthalten welche zu Auswertezeitpunkt von Maxima noch nicht mit Werten belegt sind, dürfen sie in der Berechnung nicht verwendet werden, da der Parser dann damit nichts anfangen kann.
- Solche Funktionen haben entweder im Parser eine alternative Schreibweise welche auch mit Maxima verwendet werden kann (z.B.: wenn), oder sie können prinzipell nicht verwendet werden. (Für wichtige Funktionsweisen könnte man in zukünftigen Versionen neue Funktionalitäten in den Parser einbauen, die die gewünschte Funktion erfüllen)
- Ein weiter Möglichkeit für die Verwendung solcher Funktionen ist der Verzicht auf Datensätze in diesen Funktionen, damit diese Funktion beim Auswerten des Maxima-Feldes bereits ausgewertet werden kann und somit der Parser davon nichts mehr sieht.
- zB:
if then
Infix Operatoren
arithmetische Operatoren
| Operator | Priorität | Beschreibung | Beispiel | Ergebnis |
| + | 40 | Addition | 4+5 | 9 |
| - | 40 | Subtraktion | 6-2 | 4 |
| * | 50 | Multiplikation | 4*5 | 20 |
| / | 51 | Division | 20/4 | 5 |
| % | 51 | Divisionsrest | 104%20 | 4 |
| / / | 60 | Parallelschaltung | x / / y | x*y/(x+y) |
| ^ | 90 | Potenz | 2^3 | 8 |
| .*. | 200 | Operator der intern für eine fehlende bindende Multiplikation verwendet wird | 4x | 4*x |
Bitoperatoren
| Operator | Priorität | Beschreibung | Beispiel | Ergebnis |
| | | 20 | Bitweise oder logisches ODER | 9|5 true|false |
13 true |
| or | 20 | Bitweise oder logisches ODER | 9 or 5 | 13 |
| & | 21 | Bitweise oder logisches UND | 13&10 | 8 |
| and | 21 | Bitweise oder logisches UND | 13 and 10 | 8 |
| xor | 22 | Bitweise oder logisches exklusiv oder XOR | 13 xor 10 | 7 |
| imp | 23 | Bitweise oder logisches impliziert IMP | 13 imp 10 | 8 |
| << | 35 | Bitweise links schieben | 5<<2 | 20 |
| >> | 35 | Bitweise rechts schieben | 8>>2 | 2 |
Vergleichsoperatoren
| Operator | Priorität | Beschreibung | Beispiel |
| = | 3 | Gleichungsoperator | x=y |
| == | 30 | Gleichungsoperator | x==y |
| != | 30 | Ungleichungsoperator | x!=y |
| < | 32 | Kleiner | x<y |
| <= | 32 | Kleiner gleich | x<=y |
| > | 32 | größer | x>y |
| >= | 32 | größer gleich | x>=y |
Organisative Operatoren
| Operator | Priorität | Beschreibung | Beispiel | Ergebnis |
| , | 0 | Listen-Trennzeichen | x,y | |
| $ | 1 | Trennzeichen zwischen mehreren Berechnungen | ||
| ; | 1 | Trennzeichen zwischen mehreren Berechnungen | ||
| : | 2 | Zuweisung an eine Variablen auf der linken Seite | x:5 |
Prefix Operatoren
| Operator | Priorität | Beschreibung | Beispiel | Ergebnis |
| + | 45 | positives Vorzeichen | +5 | 5 |
| - | 45 | negatives Vorzeichen | -(-5) | 5 |
| ~ | 95 | bitweise Inversion einer 64bit-Ganzzahl | ~0x0F0F | 0xFFFFFFFFFFFFF0F0 |
| ! | 120 | logisches NOT | !(3<4) | false |
| ++ | 130 | Inkrement von Ganzzahlen | ++x | erhöht x um eins und gibt das Ergebnis nach der Erhöhung zurück |
| -- | 130 | Dekrement von Ganzzahlen | --x | vermindert x um eins und gibt das Ergebnis nach der Verminderung zurück |
| % | 200 | Prefix für Namen, welche als Konstante definiert sind | %pi | 3.141592653589793 |
Suffix Operatoren
| Operator | Priorität | Beschreibung | Beispiel | Ergebnis |
| ++ | 135 | Inkrement von Ganzzahlen | x++ | erhöht x um eins und gibt den Variablenwert vor der Erhöhung zurück |
| -- | 135 | Dekrement von Ganzzahlen | x-- | vermindert x um eins und gibt den Variablenwert vor der Verminderung zurück |
Klammern
- () runde Klammern werden für mathematische Ausdrücke zur Klammerung verwendet
- {} geschwungene Klammer werden im Angabetext für die Namen der Datensätze verwendet
- [] eckige Klammern werden für Vektoren und Matrizen verwendet
Funktionen
Funktionen für Ganzzahlen
| Funktion | Beschreibung | Beispiel | Ergebnis |
| band | bitweises UND | band(4,12) | 4 |
| bor | bitweises ODER | bor(4,1) | 5 |
| bxor | bitweises EXKLUSIV ODER | band(4,5) | 1 |
| bimp | bitweises Parameter1 impliziert Parameter2 | bimp(13,10) | 8 |
| binv | bitweises NICHT mit 8 bit | binv(0x0F) | 0xF0 |
| shl | Schiebe Ganzzahl bitweise nach links | shl(8,2) | 32 |
| shr | Schiebe Ganzzahl bitweise nach rechts | shr(8,2) | 2 |
| div | Ganzzahldivision, Ergebnis wird abgeschnitten | div(5,2) | 2 |
| inv8 | bitweise Invertieren und die letzten 8 Bit bestimmen | inv8(0b1001) | 0b11110110 |
| inv16 | bitweise Invertieren und die letzten 16 Bit bestimmen | inv16(0xF0) | 0xFF0F |
| inv32 | bitweise Invertieren und die letzten 32 Bit bestimmen | inv32(0xF0) | 0bFFFFFF0F |
| inv64 | bitweise Invertieren und die letzten 64 Bit bestimmen | inv64(0xF0) | 0bFFFFFFFFFFFFFF0F |
| byte | Zahl in eine Ganzzahl wandeln und die letzten 8bit der Zahl Abschneiden, Einheit geht verloren | byte(34.2) | 34 |
| word | Zahl in eine Ganzzahl wandeln und die letzten 16bit der Zahl Abschneiden, Einheit geht verloren | word(34.2) | 34 |
| int | Zahl in eine Ganzzahl wandeln und die letzten 32bit der Zahl Abschneiden, Einheit geht verloren | int(34.2) | 34 |
| long | Zahl in eine Ganzzahl wandeln , Einheit geht verloren | long(34.2) | 34 |
| parity | Paritätsberechnung : parity(Parität,Codewortlänge,Datenwort[,Datenwort,....]) | parity(even,7,"xy") | |
| blockparity | Kreuz oder Blockparität : blockparity(Parität,Codewortlänge,Codewortanzahl,Datenwort[,Datenwort,....]) | blockparity(even,7,3,"abc") | |
| bcd | Wandelt in eine Long-Zahl in ein Feld aus BCD-kodierten Zahlen um | bcd(124) | [1,2,4] |
| code | Code aus mehreren Codeworten zusammensetzen : code(Codewortlänge,Datenwort[,Datenwort,....]) | code(5,4,3,5) | 0b1000001100101 |
| hamming | Bestimmt den Hamming-Abstand von mehreren Codeworten | hamming(1,2,4,8,16) | 2 |
| komplement | Bildet das Zweierkomplement mit einer negativen Zahl mit einer bestimmten Bitanzahl, fehlt die Bitanzahl, so wird ein 32Bit-2er-komplement gebildet | komplement(-5,8) | 0b11111011 |
| bitstream | Erzeugt aus einer Ganzzahl einen Bitstrom als String mit einer definierten Anzahl von Bit (MSB werden nötigenfalls mit 0 gefüllt) : bitstream(Daten,Bitanzahl) | bitstream(0x184,12) | "000110000100" |
Funktionen für rationale und Ganzzahlen
| Funktion | Beschreibung | Beispiel | Ergebnis |
| kgV | berechnet das kleinste gemeinsame Vielfache von mehreren Zahlen | kgV(3,10) | 30 |
| ggT | berechnet den größten gemeinsamen Teiler von mehreren Zahlen | ggT(12,10) | 2 |
| isprim | prüft ob die angegebene Zahl eine Primzahl ist | isprim(13) | true |
| prims | zerlegt eine Ganzzahl in ihre Primfaktoren | prims(12) | [2,2,3] |
| defracmix | zerlegt eine rationale Zahl in einen gemischten Bruch aus ganzzahligem Summanden, Zähler und Nenner als Menge Die erhaltene Menge kann mit dem Format-Modfier frac als gemischter Bruch dargestellt werden (siehe Zahlendarstellung) |
defracmix(14/12) defracmix(-15/12) defracmix(3/12) |
[1,2/12] [-1,3,12] [0,3,12] |
| defrac | zerlegt eine rationale Zahl in Zähler und Nenner als Menge Die erhaltene Menge kann mit dem Format-Modfier frac als gemischter Bruch dargestellt werden |
defrac(14/12) | [13,12] |
| frac | erzeugt aus einer Menge aus 2 oder 3 Elementen (von defrac) eine rationale Zahl | frac([3,7]) frac([1,2,3]) |
3/7 5/3 |
| mod | Modulo: Divisionsrest einer Division mit ganzzahligem Ergebnis | mod(5,2) mod(6.2,2.5) |
1 1.2 |
boolsche Funktionen
| Funktion | Beschreibung | Beispiel | Ergebnis |
| eq | gleich | eq(4,4) | true |
| eqruntime | symbolischer Vergleich, welcher symbolisch erst bei der Ergebnisberechnung ausgeführt wird. Muss verwendet werden, wenn bei Vergleichen symbolische Antworten von Schülern (Q0,Q1,...) verwendet werden. | eqruntime(x+3*y,3*y+x) | true |
| ne | ungleich | ne(6,4) | true |
| ge | größer gleich | ge(6,4) | true |
| le | kleiner gleich | le(6,4) | false |
| gt | größer | gt(6,4) | true |
| lt | kleiner | lt(6,4) | false |
| between | prüft ob Parameter1 kleiner als Parameter2 und Parameter2 kleiner als Parameter 3 | between(3,4,5) | true |
| land | logisches UND | land(a<b,b<c) | |
| lor | logisches ODER | lor(a<b,b<c) | |
| not | logisches NICHT. Vorsicht ein symbolisches Ergebnis von Maxima liefert not als Prefix-Operator, welcher vom Parser nicht unterstützt wird ( Verwende statt dessen lnot ) | not(a<b) | |
| lnot | logisches NICHT, wie not jedoch wird es von Maxima nicht ausgewertet | lnot(a<b) |
arithmetische Funktionen
| Funktion | Beschreibung | Beispiel | Ergebnis |
| double | Zahl in eine Gleitkommazahl umwandeln, die Einheit geht dabei verloren | double(3.4V) | 3.4 |
| numeric | verwirft die Einheit, wenn eine vorhanden ist und liefert nur den Zahlenwert | numeric(2.3mA) numeric(5%) |
0.0023 5 |
| unit | gibt die SI-Einheit mit dem Zahlenwert 1 zurück | unit(3.1kA) unit(5%) |
1A 1% |
| cround | Rundet die Zahl kaufmännisch, der zweite Parameter gibt die Anzahl der Kommastellen an, ohne 2.Parameter wird auf Ganzzahlen gerundet, bei komplexen Zahlen wird Betrag und Winkel in Grad gerundet. | cround(23.535,2) cround(2.435arg34.5364°,1) |
23.54 2.4arg34.5° |
| ccround | Rundet die Zahl kaufmännisch, der zweite Parameter gibt die Anzahl der Kommastellen an, bei komplexe Zahlen wird Real und Imaginärteil gerundet. | ccround(2.4534+5.645*%i,2) | 2.45+5.65i |
| round | Rundet die Zahl kaufmännisch, aus Kompatibilitätsgründen zu Maxima hat round nur einen Parameter | round(23.535) | 24 |
| ground | Rundet die Zahl auf die im zweiten Parameter angegebenen gültigen Ziffern | ground(2453.43,2) | 2500 |
| floor | Rundet auf die größte ganze Zahl, welche kleiner oder gleich x ist | floor(24.5) | 24 |
| trunc | Schneidet die Zahl nach dem Komma ab | trunc(24.5) | 24 |
| ceiling | ceiling(x) Rundet auf die kleinste ganze Zahl, welche größer oder gleich x ist | ceiling(13.2) | 14 |
| pow | Potenzfunktion | pow(2,3) | 8 |
| par | Parallelschaltung von Widerständen | par(x,y) | x*y/(x+y) |
| min | Minimum von mehrere Werten suchen | min(3,5,1) | 1 |
| max | Maximum von mehreren Werten suchen | max(3,5,1) | 5 |
| random | Zufallszahl aus einem definierten Zahlenbereich random(minimal,maximal) VORSICHT! Die Zufallszahl wird bei jedem Aufruf neu berechnet, weshalb sich der Wert bei jedem Anzeigevorgang einer Frage ändert. Sollte sich der berechnete Wert für eine Schülerangabe zwischen Fragestellung und Ergebniskontrolle nicht ändern dürfen (ist der Normalfall) muss man einen Datensatz statt einer Zufallszahl verwenden! Zufallszahlen haben in der Ergebnisberechnung keinen Sinn, und sollten maximal für angezeigte zufällige Werte verwendet werden! |
random(2,8) | 3.4532 |
| randomC | komplexe Zufallszahl aus einem definierten Zahlenbereich für den Betrag VORSICHT! Die Zufallszahl wird bei jedem Aufruf neu berechnet! |
randomC(2,8) | 3.4532arg40.3° |
| signum | Liefert das Vorzeichen einer Zahl (-1,0,1). Bei einer komplexen Zahl das Vorzeichen des Realteils. | signum(-4) | -1 |
Maxima-basierte Funktionen
- Diese Funktionen funktionieren nur wenn Maxima installiert ist und werden immer an Maxima gesendet, auch wenn der interne Parser aktiviert ist.
- Weiters werden sie bei der Ausgabe als TeX-Formel auch korrekt mit LaTeX gesetzt.
| Funktion | Beschreibung | Beispiel | Ergebnis |
| integrate | Berechnet das unbestimmte oder bestimmte Integral einer Funktion. | integrate(x^2,x) integrate(x^2,x,0,2) |
x^3/3 8/3 |
| diff | Berechnet die Ableitung einer Funktion. | diff(x^2,x) diff(3*x^2,x,2) |
x 6 |
| tomaxima | Führt die Berechnung aller Parameter von links nach rechts hintereinander mit Maxima aus. Das Ergebnis ist dann das Ergebnis des letzten Parameters. | tomaxima(y:x^2,y+2) | x^2+2 |
| laplace | Bestimmt die Laplace-Transformierte einer Funktion. | laplace(sin(t),t,s) | 1/(1+s^2) |
| ilt | Bestimmt die inverse Laplace-Transformierte eine Laplace-Funktion | ilt(1/(1+s),s,t) | e^(-t) |
| sum | Summenbildung | sum(1/k,k,1,2) | 3/2 |
| product | Produktbildung | product(1/k,k,1,3) | 1/6 |
erweiterte arithmetische Funktionen
Stringfunktionen
| Funktion | Beschreibung | Beispiel | Ergebnis |
| dechex | Zahl in eine Ganzzahl wandeln und als Hexadezimal-String ausgeben | dexhex(12) | "0xC" |
| chr | Bestimmt die Zeichen mit dem ASC-II-Code der Long-Parameter und setzt daraus einen String zusammen. | chr(0x65,105) | "ei" |
| val | Bestimmt den ASC-II-Code des ersten Zeichens welches als String-Parameter übergeben wurde. | val("a") | 97 |
| strcat | Fügt mehrere Strings zusammen. | strcat("a","b") | "ab" |
trigonometrische Funktionen
| Funktion | Beschreibung | Beispiel | Ergebnis |
| sin | Sinus | sin(%pi/2) | 1 |
| cos | Cosinus | cos(%pi/2) | 0 |
| tan | Tangens | tan(%pi/4) | 1 |
| asin | Arcus-Sinus | asin(1) | %pi/2 |
| arcsin | Arcus-Sinus | asin(1) | %pi/2 |
| acos | Arcus-Cosinus | acos(1) | 0 |
| arccos | Arcus-Cosinus | acos(1) | 0 |
| atan | Arcus-Tangens | atan(1) | %pi/4 |
| arctan | Arcus-Tangens | arctan(1) | %pi/4 |
| atan2 | Arcus-Tangens atan2(y,x)=arctan(y/x) | atan2(-2,-2) | -%pi*3/4 |
| arctan2 | Arcus-Tangens arctan2(y,x)=arctan(y/x) | arctan2(-2,-2) | -%pi*3/4 |
| sinh | Sinus-Hyperbolicus | sinh(1) | 1.1752012 |
| cosh | Cosinus-Hyperbolicus | cosh(1) | 1.5430806 |
| tanh | Tangens-Hyperbolicus | tanh(1) | 0.7615941 |
| coth | Cotangens-Hyperbolicus | coth(1) | 1.313035 |
| asinh | Area-Sinus-Hyperbolicus | asinh(1.1752012) | 1 |
| acosh | Area-Cosinus-Hyperbolicus | acosh(1.5430806) | 1 |
| atanh | Area-Tangens-Hyperbolicus | atanh(0.7615941) | 1 |
| acoth | Area-Cotangens-Hyperbolicus | acoth(1.313035) | 1 |
| csin | Erzeugt aus einer komplexen Zahl (Effektivwert) und einer Frequenz einen Sinusfunktion in der Zeit | csin(U) | sqrt(2)*cabs(U)*sin(2*pi*f*t+carg(U)) |
| quadrant | Liefert den Quadranten eines Winkels mit einer Toleranzangabe. | quadrant(20°,5°) | 1 |
| argnorm | Wandelt einen Winkel auf den Bereich von 0°-360° | argnorm(-50°) | 310° |
Exponentialfunktionen
| Funktion | Beschreibung | Beispiel | Ergebnis |
| pow | Potenzfunktion | pow(2,3) | 8 |
| exp | Exponentialfunktion | exp(1) | %e |
| log | natürlicher Logarythmus | log(%e) | 1 |
| ln | natürlicher Logarythmus | ln(%e) | 1 |
| log10 | Logarythmus zur Basis 10 | log10(100) | 2 |
komplexe Zahlen
Die Funktionen zu komplexen Zahlen werden (anders als in Maxima) nur ausgewertet wenn das Ergebnis numerisch berechenbar ist, ansonsten bleibt die Funktion symbolisch erhalten.
| Funktion | Beschreibung | Beispiel | Ergebnis |
| abs | Liefert den Absolutbetrag einer komplexen Zahl | abs(3+4*%i) | 5 |
| cabs | Liefert den Absolutbetrag einer komplexen Zahl | cabs(3+4*%i) | 5 |
| carg | Liefert das Argument einer komplexen Zahl | carg(4*%e^(3*%i)) | 3 |
| realpart | Liefert den Realteil einer komplexen Zahl | realpart(3+4*%i) | 3 |
| imagpart | Liefert den Imaginärteil einer komplexen Zahl | imagpart(3+4*%i) | 4 |
| conjugate | Liefert die konjugiert komplexe Zahl einer komplexen Zahl | conjugate(3+4*%i) | 3-4*%i |
| rectform | hat in LeTTo keine Relevanz, da die Zahlendarstellung bei der Ausgabe definiert wird wie zB.: {=3arg2;karti} |
statistische Funktionen
Die Funktionen funktionieren nur ohne Einheiten.
| Funktion | Beschreibung | Beispiel | Ergebnis |
| factorial | Liefert die Fakultät einer positiven ganzen Zahl | factorial(5) | 120 |
| binomial | Liefert den Binomialkoeffizienten von zwei positiven ganzen Zahlen | binomial(5,2) | 10 |
Mengen-Funktionen
Mengen werden intern als Vektoren verarbeitet und sind deshalb auch direkt durch Vektoren ersetzbar. Auch alle Vektor-Funktionen sind somit auch auf Mengen anwendbar und umgekehrt.
| Funktion | Beschreibung | Beispiel | Ergebnis | ab Rev |
| setget | Liefert ein Element einer Menge oder einer Matrix (Menge von Mengen) | setget([12,13,14],1) setget(matrix([9,2],[3,4]),0,1) |
13 2 | |
| setset | setzt ein Element einer Menge oder einer Matrix (Menge von Mengen) | setset([12,13,14],1,35) setset(matrix([9,2],[3,4]),0,0,-9) |
[12,35,14] [[-9,2],[3,4]] | |
| setlength | liefert die Anzahl der Elemente einer Liste, Menge oder eines Vektors | setlength([3,6,54,34,3,54]) | 6 | |
| setinsert | fügt ein Element in eine Menge an eine gegebene Stelle ein | setinsert([12,13,14],1,25) | [12,25,13,14] | |
| setremove | löscht ein Element einer Menge | setremove([12,13,14],1) | [12,14] | |
| setapply | wendet einen Ausdruck oder Funktion auf alle Elemente einer Menge an | setapply(y,[1,2,3],y*2) | [2,4,6] | 5965 |
| setmedian | Liefert den Median einer Menge | setmedian([4,3,1,5,6]) | 4 | |
| setboxplot | Liefert die Werte des Boxplot einer Menge (Minimum, unteres Quartil, Median, oberes Quartil, Maximum) als Vektor verwendbar für das Plot-Plugin | setboxplot([1,2,3,10,8,9]) | [1,2,5.5,9,10] | |
| setsort | Sortiert die Elemente einer Menge aufsteigend | setsort([3,-3,2,0,5,2]) | [-3,0,2,2,3,5] | |
| setsortnd | Sortiert die Elemente einer Menge aufsteigend und entfernt alle mehrfach vorkommenden Elemente | setsortnd([31,-3,2,31,0,5,2]) | [-3,0,2,5,31] | |
| setcount | Bestimmt die Anzahl wie oft ein Element in einer Menge vorkommt oder die Anzahl der Elemente der Menge | setcount([31,-3,2,31,0,5,2],31) setcount([2,5,3,6]) |
2 4 | |
| setmodus | Liefert das Element einer Menge, welches am öftesten vorkommt oder die Elemente als Menge wenn mehrere Elemente gleich oft vorkommen | setmodus([3,-3,2,0,5,2]) | 2 | |
| setreverse | Dreht die Reihenfolge einer Menge um | setreverse([3,-3,2,0,5,2]) | [2,5,0,2,-3,3] | |
| setnd | Löscht alle Duplikate aus der Menge | setnd([3,-3,2,0,5,2]) | [3,-3,2,0,5] | |
| setshuffle | Mischt eine Menge in eine zufällige Reihenfolge | setshuffle([3,-3,2,0,5,2]) | [2,0,5,-3,2,3] | |
| setmittel | Bestimmt den Mittelwert einer Menge | setmittel([1,3,2,4]) | 2.5 | |
| setgeomittel | Bestimmt das geometrische Mittelwert einer Menge aus positiven reellen Zahlen | setgeomittel([10,20,30]) | 18.171206 | |
| setvarianz | Bestimmt die empirische Varianz einer Menge | setvarianz([3,1,2,5,4]) | ((3-3)^2+(1-3)^2+(2-3)^2+(5-3)^2+(4-3)^2)/5=2 | |
| setquadratmittel | Bestimmt den quadratischen Mittelwert einer Menge | setquadratmittel([10,20,30]) | 21.6025 | |
| setsum | Bestimmt die Summe aller Werte einer Menge | setsum([1,3,2,4]) | 10 | |
| setprod | Bestimmt das Produkt aller Werte einer Menge | setprod([1,3,2,4]) | 24 | |
| setunion | Fügt mehrere Mengen zu einer neuen Menge zusammen | setunion([1,3,2,4],[3,7]) | {1,3,2,4,3,7} | |
| setunionnd | Fügt mehrere Mengen zu einer neuen Menge zusammen, sortiert diese und entfernt alle mehrfachen Elemente | setunionnd([1,3,2,4],[3,7]) | {1,2,3,4,7} | |
| setcut | Bildet die Schnittmenge aus mehreren Mengen | setcut([1,3,2,4],[3,7]) | {3} | |
| setcompare | vergleicht zwei Mengen miteinander, wobei die Reihenfolge egal ist | setcompare([1,3,2,4],[3,7]) setcompare([1,3,2],[1,2,3]) setcompare([1,3,2],[1,3,2,3]) setcompare([1,2,3],[1,2,3]) |
false true false true | |
| setcomparend | vergleicht zwei Mengen miteinander, wobei die Reihenfolge egal ist und doppelte Werte als einfach behandelt werden. | setcomparend([1,3,2,4],[3,7]) setcomparend([1,3,2],[1,2,3]) setcomparend([1,3,2],[1,3,2,3]) setcomparend([1,2,3],[1,2,3]) |
false true true true | |
| setpartof | prüft ob die erste Menge eine Teilmenge der zweite Menge ist wobei die Reihenfolge egal ist aber mehrfache Werte berücksichtigt werden | setpartof([1,4],[1,3,7]) setpartof([1,3],[1,2,3]) setpartof([1,3,3],[1,3,5,7]) setpartof([1,4,4],[1,2,3,4]) |
false true false false | |
| setpartofnd | prüft ob die erste Menge eine Teilmenge der zweite Menge ist wobei die Reihenfolge und mehrfache Werte egal sind | setpartofnd([1,4],[1,3,7]) setpartofnd([1,3],[1,2,3]) setpartofnd([1,3,3],[1,3,5,7]) setpartofnd([1,4,4],[1,2,3,4]) |
false true true true | |
| setgetmin | Liefert den kleinsten Wert einer Menge | setgetmin([1,3,-2,4]) | -2 | |
| setgetmax | Liefert den größten Wert einer Menge | setgetmax([1,3,-2,4]) | 4 | |
| setremovefirst | Entfernt den ersten Wert einer Menge | setremovefirst([1,3,-2,4]) | {3,-2,4} | |
| setremovelast | Entfernt den letzten Wert einer Menge | setremovelast([1,3,-2,4]) | {1,3,-2} | |
| setgetfirst | Liefert den ersten Wert einer Menge | setgetfirst([1,3,-2,4]) | 1 | |
| setgetlast | Liefert den letzten Wert einer Menge | setgetlast([1,3,-2,4]) | 4 | |
| setsub | setsub(M,x,y) Liefert eine Teilmenge von M der Elemente vom index x bis zum Index y | setsub([1,3,-2,4],1,2) | {3,-2} | |
| setmakelist | setmakelist(f,x,start,stop) setzt in den Ausdruck f für x die Werte von start bis stop mit einer Schrittweite von 1 ein. | setmakelist(x^2,x,1,4) | [ 1,4,9,16 ] | |
| setmakelist(f,x,start,stop,schrittweite) setzt in den Ausdruck f für x die Werte von start bis stop mit dem Abstand schrittweite ein. | setmakelist(x^2,x,1,2,0.5) | [ 1,2.25,4 ] | ||
| setmakelist(f,x,set) setzt die Werte des Vektors set in den Ausdruck f für x ein. | setmakelist(x^2,x,[3,1,2]) | [ 9,1,4 ] | ||
| foreach | Führt für jedes Element eine Berechnung aus und verbindet die Ergebnisse mit der Aggregatfunktion | foreach([2,-3,5,-6],p,cabs(p),"+") | 16 | 6075 |
Punkte-Mengen-Funktionen
Bei der Eingabe mit dem Plot-Plugin werden Punkte-Mengen als Matrizen in der Form [[x1,y1],[x2,y2],[y3,y3]] für die gespeicherten Punkte welcher der Schüler eingegeben hat verwendet.
Um die Verarbeitung der Eingaben zu erleichtern kann man die Funktionen beginnend mit pv verwenden.
| Funktion | Beschreibung | Beispiel | Ergebnis | ab Rev |
| pvlineabs | Bestimmt aus dem n-ten Punktepaar den Absolutbetrag des Abstandes. | pvlineabs([[2,3],[4,5],[6,3],[-2,4]],0) | 2.82842712475 | 6075 |
| pvlinearg | Bestimmt aus dem n-ten Punktepaar den Winkel der Strecke zur x-Achse | pvlinearg([[2,3],[4,5],[6,3],[-2,4]],0) | 45° | 6075 |
| pvlinek | Bestimmt die Steigung der zugehörigen Geraden dem n-ten Punktepaar | pvlinek([[2,3],[4,5],[6,3],[-2,4]],0) | 1 | 6075 |
| pvlined | Bestimmt den Schnittpunkt einer Geraden durch das n-te Punktepaar mit der y-Achse | pvlined([[2,3],[4,5],[6,3],[-2,4]],0) | 1 | 6075 |
| pvline | Bestimmt die Geradengleichung einer Geraden durch das n-te Punktepaar | pvline([[2,3],[4,5],[6,3],[-2,4]],0) | y=x+1 | 6075 |
| pvpoints | Bestimmt die Anzahl der Punkte | pvpoints([[2,3],[4,5],[6,3],[-2,4]]) | 4 | 6075 |
| pvvect | Bestimmt einen Vector aus dem n-te Punktepaar | pvvect([[2,3],[4,5],[6,3],[-2,4]],0) | [2,2] | 6075 |
| pvforeachline | Führt für jedes Punktepaar eine Berechnung aus und verbindet die Ergebnisse mit der Aggregatfunktion | pvforeachline([[2,3],[4,5],[6,3],[-2,4]],p,pvlineabs(p),"+") | 10.890684873 | 6075 |
Typ-Funktionen
Werden nur dann ausgewertet wenn der Parameter ein numerischer Wert oder eine Menge ist.
| Funktion | Beschreibung | Beispiel | Ergebnis |
| isset | Prüft ob es sich um eine Menge handelt. | isset([12,13,14]) | true |
| issetnumeric | Prüft ob es sich um eine Menge aus reellen Zahlen handelt. | issetnumeric([12,13.4,14]) | true |
| issetlong | Prüft ob es sich um eine Menge aus ganzen Zahlen handelt. | issetlong([12,13,14]) | true |
| islong | Prüft ob es sich um eine ganze Zahl handelt. | islong(12) | true |
Algebra
Hinweis: Die Indizes eines Vektors oder einer Matrix werden in Letto ausgehend von 0 weg gezählt.
| Funktion | Beschreibung | Beispiel | Ergebnis |
| matrix | erzeugt aus mehreren gleich langen Vektoren eine Matrix | matrix([1,2],[3,4]) | [[1,2],[3,4]] |
| inv | invertiert eine quadratische Matrix oder bildet 1/x | inv(matrix([1,2],[3,4])) | [[-2,1],[3/2,-1/2]] |
| vget | liefert ein Element eines Vektors oder einer Matrix Video | vget([12,13,14],1) vget(matrix([9,2],[3,4]),0,1) |
13 2 |
| vset | setzt ein Element eines Vektors oder einer Matrix | vset([12,13,14],1,35) vset(matrix([9,2],[3,4]),0,0,-9) |
[12,35,14] [[-9,2],[3,4]] |
| vinsert | fügt ein Element in einen Vektor an eine gegebene Stelle ein | vinsert([12,13,14],1,25) | [12,25,13,14] |
| vremove | löscht ein Element eines Vektors Video | vremove([12,13,14],1) | [12,14] |
| vabs | Berechnet den Betrag eines Vektors | vabs([3,4]) | 5 |
| vin | Berechnet das innere Produkt von 2 Vektoren | vin([1,2,3],[4,5,6]) | 32 |
| vex | Berechnet das ex-Produkt von 2 Vektoren im 3-dimensionalen Raum | vex([1,2,3],[4,5,6]) | [-3,6,-3] |
| mrows | liefert die Anzahl der Zeilen einer Matrix | mrows([[3,4,4],[3,6,54,34,3,54]]) | 2 |
| mcols | liefert die Anzahl der Spalten einer Matrix | mcols([[3,4,4],[3,6,54,34,3,54]]) | 6 |
| mprod | Bildet das Matrixprodukt aus zwei Matrizen | mprod([[1,2],[3,4]],[[5,6],[7,8]]) | [[19,22],[43,50]] |
| mtrans | Bildet die transponierte Matrix | mtrans([[1,2],[3,4]]) | [[1,3],[2,4]] |
| minv | Bildet die inverse Matrix | minv([[1,2],[3,4]]) | [[-2,1],[3/2,-1/2]] |
| mdet | Bildet die Determinante einer quadratischen Matrix | mdet([[1,2],[3,4]]) | -2 |
| vindex | vindex(v,x) liefert den Index des Elementes eines Vektors, welcher am nächsten bei x liegt | vindex([10,30,70],40) | 1 |
| vindexup | vindexup(v,x) liefert den Index des Elementes eines Vektors, welcher größer oder gleich x ist | vindexup([10,30,70],40) | 2 |
| vindexdown | vindexdown(v,x) liefert den Index des Elementes eines Vektors, welcher kleiner oder gleich x ist | vindexdown([10,30,70],60) | 1 |
| verweis | verweis(M,x,n) liefert den Wert der n-ten Spalte (ohne Angabe von n die 2.Spalte) einer Matrix M wo x dem Wert in der ersten Spalte am nächsten liegt | verweis([[10,33],[20,77],[30,99]],21) | 77 |
| verweisup | verweisup(M,x,n) liefert den Wert der n-ten Spalte (ohne Angabe von n die 2.Spalte) einer Matrix M wo x dem Wert in der ersten Spalte am nächsten liegt | verweisup([[10,33],[20,77],[30,99]],21) | 99 |
| verweisdown | verweisdown(M,x,n) liefert den Wert der n-ten Spalte (ohne Angabe von n die 2.Spalte) einer Matrix M wo x dem Wert in der ersten Spalte am nächsten liegt | verweisdown([[10,33],[20,77],[30,99]],27,1) | 77 |
Variable
| Funktion | Beschreibung | Beispiel | Ergebnis |
| kill | löscht Variable aus dem Variablenspeicher | kill(x,y) kill(allbut(y)) kill(all) |
löscht die Variablen x und y löscht alle Variablen mit Ausnahme von y löscht alle Variable |
| allbut | Liefert eine Liste aller Variablen des Parsers als Menge(Vektor) mit Ausnahme der als Parameter angegebenen Variablen | allbut(x,y) | [a,b,c] |
Auswertung und Programmierung
| Funktion | Beschreibung | Beispiel | Ergebnis | Revision |
| ev | Auswertung eines Ausdruckes, als Parameter können Gleichungen angegeben werden, welche dann in den Ausdruck eingesetzt werden | ev(x*y,y=4) | x*4 | |
| evruntime | Auswertung eines Ausdruckes, als Parameter können Gleichungen angegeben werden, welche dann in den Ausdruck eingesetzt werden. Das Einsetzen erfolgt erst bei der Ergebnisberechnung! | evruntime(x*y,y=4) | x*4 | |
| nv | Auswertung eines Ausdruckes, als Parameter können Gleichungen angegeben werden, welche dann in den Ausdruck eingesetzt werden. Im Gegensatz zu ev werden bestehende Variable nur in den Gleichungen, aber nicht im Ausdruck selbst eingesetzt! | nv(x*y,y=4) | x*4 | |
| if | Bedingungsfunktion if(bedingung,wahrwert,falschwert) | if(4<6,10,12) | 10 | |
| wenn | Bedingungsfunktion wenn(bedingung,wahrwert,falschwert). Im Prinzip identisch wie if, jedoch kann if mit Maxima nicht verwendet werden. | wenn(4<6,10,12) | 10 | |
| plugin | Ruft die Berechnungsmethode des Plugins, welches als erster Stringparameter angegeben werden muss auf und übergibt die weiteren Parameter an die Berechnungsmethode des Plugins. | plugin("plugin1",3) | führt die Berechnung des Plugins mit dem Namen "plugin1" mit dem Parameter 3 aus. | |
| symbolic | Bei allen Variablen innerhalb von symbolic werden nur nicht-numerische Werte eingesetzt! Wird vor allem im Angabtext bei {= } verwendet | symbolic(x^2+2) | x^2+2 | |
| runtime | Bei dieser Funktion wird erst bei der Berechnung der Frageantwort, nach dem Einsetzen der Datensätze das komplette Maxima-Feld mit dem internen Parser durchgerechnet und danach der Parameter-Ausdruck berechnet. Dadurch kann man bei komplizierten Berechnungen eine sehr aufwendige symbolische Berechnung verhindern! | runtime(U) | ||
| dataset | liefert alle Datensätze einer Datensatz-Definition in einem Vektor | dataset(x) | ||
| parse | Wenn der Parameter ein String ist wird dieser String mit dem Parser interpretiert | parse("2+3") | 5 | |
| foreach | Führt für jedes Element einer Menge eine Berechnung aus und verbindet die Ergebnisse mit der Aggregatfunktion | foreach([2,-3,5,-6],p,cabs(p),"+") | 16 | 6075 |
| pvforeachline | Führt für jedes Punktepaar einer Punktemenge eine Berechnung aus und verbindet die Ergebnisse mit der Aggregatfunktion | pvforeachline([[2,3],[4,5],[6,3],[-2,4]],p,pvlineabs(p),"+") | 10.890684873 | 6075 |
| loop | Führt eine Zählschleife aus loop(Variable,Startwert,Wiederholbedingung,Inkrement,Ausdruck,Aggregatsfunktion). Ohne Aggregatsfunktion wird ein Feld mit den Ergebnissen der Schleifeniterationen geliefert. |
loop(i,1,i<7,i++,i,"+") loop(i,1,i<7,i:i+2,i) |
21 [1,3,5] |
6077 |
Optimierung der Ausdrücke
| Funktion | Beschreibung | Beispiel | Ergebnis |
| opt | Ausdruck wird vollständig optimiert, die Funktion wird ausgewertet und ist danach nicht mehr vorhanden. Nur bei der Verwendung des internen Parser sinnvoll. | opt(x+x) | 2*x |
| ratsimp | Ausdruck wird vollständig optimiert, die Funktion wird ausgewertet und ist danach nicht mehr vorhanden (wie opt, wird jedoch auch von Maxima ausgewertet) | ratsimp(x+x) | 2*x |
| noopt | Ausdruck wird nicht optimiert, bleibt also so erhalten wie angegeben. Die Funktion an sich geht aber verloren. | noopt(2+3) | 2+3 |
| nopt | Ausdruck wird nicht optimiert, bleibt also so erhalten wie angegeben. Die Funktion bleibt erhalten und wird erst bei der Lösungsberechnung oder durch opt() entfernt. | noopt(2+3) | 2+3 |
| lopt | Im Maximafeld bleibt die Funktion ohne Funktion erhalten, im Ergebnis {= wird die Funktion entfernt und in der Lösung wird nach dem Einsetzen der Werte der Ausdruck vollständig optimiert. | lopt(x+3) | lopt(x+3) |
| lnoopt | Im Maximafeld bleibt die Funktion ohne Funktion erhalten, im Ergebnis {= wird die Funktion entfernt und in der Lösung wird nach dem Einsetzen der Werte der Ausdruck nicht mehr optimiert. | lnoopt(x+3+2) | lnoopt(x+5) |
| loptnumeric | Im Maximafeld bleibt die Funktion ohne Funktion erhalten, im Ergebnis {= wird die Funktion entfernt und in der Lösung wird nach dem Einsetzen der Werte der Ausdruck nur numerisch optimiert. | loptnumeric(x+y) | loptnumeric(x+y) |
| aopt | Bei Maxima und Lösung geht die Funktion verloren, nur innerhalb von noopt bleibt sie erhalten. Bei der Anzeige führt sie zur Optimierung das Ausdruckes nach Einsetzen der Datensätze. | aopt(x) | x |
Anzeige und Lösungsberechnung
Diese Funktionen haben entweder einen oder zwei Parameter. Der erste Parameter stellt die darzustellende Funktion dar, der zweite Parameter, welcher eine Ganzzahl sein muss, gibt an, wie die Darstellung erfolgen soll. Wird der 2.Parameter weggelassen, so wird er als 0 interpretiert.
- 0 Bei Berechnungen hat die Funktion keine Wirkung, bleibt aber als Funktion erhalten. Bei Lösung und Anzeige wird die Funktion ausgewertet
- 1 Wirkt nur bei Lösung, bei Berechnungen bleibt die Funktion erhalten
- 2 Wirkt nur bei Anzeige, bei Berechnungen bleibt die Funktion erhalten
| Funktion | Beschreibung | Beispiel | Ergebnis |
| viewpow | Gibt alle Wurzeln als Potenzen aus, und stellt alle Potenzen im Nenner als negativen Exponenten im Zähler dar | viewpow(sqrt(x)) | x^(1/2) |
| viewsqrt | Gibt Potenzen welche als Wurzel darstellbar sind auch als als Wurzeln mit der Funktion sqrt oder root aus | viewsqrt(x^(1/2)) | sqrt(x) |
Spezialfunktionen LeTTo
| Funktion | Beschreibung | Beispiel | Ergebnis |
| points | Berechnet die erreichbare Gesamtpunkteanzahl einer Frage | points() | 2 |
| points | Berechnet die erreichbare Punkteanzahl einer Teilfrage. Als Parameter wird die Fragenummer als Ganzzahl angegeben. | points(0) | 1 |
Spezialfunktionen Technik
| Funktion | Beschreibung | Beispiel | Ergebnis |
| color | Widerstandsfarbcode berechnen. 1. Parameter muss ein Double sein 2.Parameter sind die Anzahl der Farbringe 3.Parameter ist der Modus (0..2-St,1..3St,2..Deutsch,3..2StEng,4..3StEng,5..Englisch |
color(120,3,2) | braun,rot,braun |
| parsecolor | Wandelt einen String mit einem Widerstandsfarbcode in einen Double-Wert | parsecolor("br-rt-br") | 120 |
| ip | Wandelt eine Long-Zahl in einen String als IP-Adresse um, oder 4 Byte-Zahlen in eine Long Zahl als IP-32-bit-Adresse | ip(1534536453) ip(10,20,30,40) |
"91.119.43.5" 169090600 |
| parseip | Wandelt einen String mit einer IP-Adresse in einen Long-Wert | parseip("91.119.43.5") | 1534536453 |
| e12 | rundet einen Zahlenwert auf den nächstliegenden Wert der Normreihe E12. Die Rundung erfolgt geometrisch d.h. der Quotient zwischen Normwert und zu rundendem Wert wird minimiert. |
e12(700Ohm) | 680Ohm |
| e12up | rundet einen Zahlenwert auf den nächstgrößerern Wert der Normreihe E12 | e12(670Ohm) | 680Ohm |
| e12down | rundet einen Zahlenwert auf den nächstkleineren Wert der Normreihe E12 | e12(700Ohm) | 680Ohm |
| ise12 | prüft ob der als Parameter übergebenen Wert ein Wert der Normreihe E12 ist. | ise12(680Ohm) | true |
| norm | rundet einen Zahlenwert auf den nächstliegenden Wert einer gegebenen Wertereihe oder Normreihe. Die Rundung erfolgt geometrisch wenn es sich um eine logarithmisch aufgeteilte Normreihe handelt, oder sonst linear. |
norm(700Ohm,E12) | 680Ohm |
| normup | rundet einen Zahlenwert auf den nächstgrößerern Wert einer gegebenen Wertereihe oder Normreihe. | normup(730Ohm,[1,3,5,8]) | 800Ohm |
| normdown | rundet einen Zahlenwert auf den nächstkleineren Wert einer gegebenen Wertereihe oder Normreihe. | normdown(700Ohm,E12) | 680Ohm |
| isnorm | prüft ob der als Parameter übergebenen Wert ein Wert einer gegebenen Wertereihe oder Normreihe ist. | isnorm(680Ohm,E12) | true |
Raumzeiger für elektrische Maschinen
| Funktion | Beschreibung | Beispiel | Ergebnis |
| svphtosv(a,b,c) | berechnet aus den Stranggrößen (a,b,c) einen komplexen Raumzeiger | svphtosv(0.5,0.5,-1) | 1arg60° |
| svsvtoph(sv) svsvtoph(sv,index) |
berechnet aus einem komplexen Rauzeiger die Phasengrößen berechnet aus einem komplexen Rauzeiger die Phasengrößen, index selektiert Stranggröße als Rückgabewert |
svsvtoph(1arg60°) svsvtoph(1arg60°,3) |
[0.5,0.5,-1] -1 |
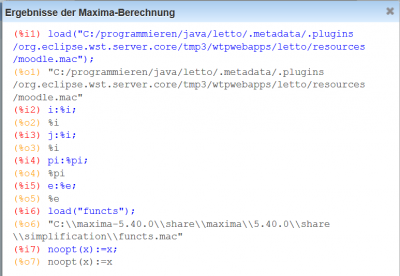
Ergebnisvorschau
Aufruf dieses Dialoges über den -Button aus dem Toolbar.
Die Berechnungen aus dem Maxima-Feld bei der Fragendefinition können auch über den -Button durchgeführt werden. Hier wird die Berechnung durchgeführt und das Lösungsfeld ausgefüllt, aber der Rechengang wird nicht angezeigt.
Beim Fehlersuchen oder bei komplexen Berechnungen kann es aber hilfreich sein, den ganzen Maxima-Lösungsweg zu sehen, dies ist über den -Button möchlich.