Datensätze definieren: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Mayer (Diskussion | Beiträge) |
Mayer (Diskussion | Beiträge) |
||
| Zeile 7: | Zeile 7: | ||
==Erstellung / Änderung über den Datensatz-Bereich== | ==Erstellung / Änderung über den Datensatz-Bereich== | ||
:[[Datei:ClipCapIt-180620-222938.PNG]] | :[[Datei:ClipCapIt-180620-222938.PNG|300px]] | ||
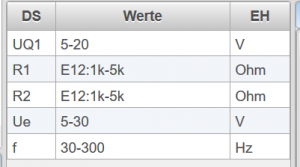
Die Tabelle zur Definition der Datensätze enthält drei Spalten: | Die Tabelle zur Definition der Datensätze enthält drei Spalten: | ||
* DS: Name der Variable | * DS: Name der Variable | ||
| Zeile 13: | Zeile 13: | ||
* EH: Einheit der Variable | * EH: Einheit der Variable | ||
Über das [[Kontext-Menü]] diese Datensatz-Bereichs in der Oberfläche können auch neue Variablen hinzugefügt werden. | |||
==Definition der Werte== | ==Definition der Werte== | ||
Version vom 20. Juni 2018, 20:32 Uhr
Einführung zu Datensätzen
Eingabe von Datensätzen
Jede Variable, die im Angabetext in geschwungenen Klammern eingesetzt werden kann, wird über einen Datensatz definiert.
Erstellung aus dem Editor
Erstellung / Änderung über den Datensatz-Bereich
Die Tabelle zur Definition der Datensätze enthält drei Spalten:
- DS: Name der Variable
- Werte: Definition des Wertebereiches und des Types der Variable
- EH: Einheit der Variable
Über das Kontext-Menü diese Datensatz-Bereichs in der Oberfläche können auch neue Variablen hinzugefügt werden.
Definition der Werte
Es gibt zwei Varianten einen Wertebereich zu definieren:
- Nur durch die Angabe eines gültigen Bereiches: zB.:1-10,E12:1k-10k
- Durch einen Typbezeichner gefolgt von einem gültigen Bereich: zB.: C:1-10
Folgende Typbezeichner sind möglich:
| Bezeichner | Beschreibung | Beispiel |
| I: | Ganzzahl | I:10-20 |
| V[Dimension]: | Vektor | V3:1-10 |
| M[Zeilen]x[Spalten]: | Matrix der Dimension [Zeilen]x[Spalten] | M3x3:1-10 |
| P[Grad]: | Polynom der Ordnung [Grad] in der Variablen s | P3:1-10 |
| B[Zählergrad],[Nennergrad]: | Polynombruch in der Variablen s mit definiertem Zählergrad und Nennergrad | B2,3:1-20 |
| C: | komplexe Zahl mit zufälligem Winkel zwischen 0° und 360° | C:1-10 |
| komplexe Zahl mit Betrag und Winkel in Grad | C:1-10arg10-90 | |
| komplexe Zahl mit Realteil und Imaginärteil | C:1-10j1-10 | |
| F[ziffern]: | Gleitkommazahl mit einer definierten Anzahl gültiger Ziffern | F3:5-9 |
| S: | Zeichenketten durch Beistrich getrennt | S:rot,grün,blau |
| R: | Regulärer Ausdruck: Erzeugt einen String auf den der reguläre Ausdruck trifft. | R:[a-m]x?[^B]+ |
| R[stellen]: | Regulärer Ausdruck erzeugt einen String mit "stellen" Zeichen | R5:.+ |
| R[minstellen]-[maxstellen]: | Regulärer Ausdruck mit einen Stellenanzahl von "minstellen" bist "maxstellen" | R5-8:[a-z]+\d+ |
| sI:wert,wert,wert | erzeugt Ganzzahl-Datensätze aus den angegebenen Werten, wobei die Reihenfolge der Werte wie angegeben beibehalten wird! (Zahlenbereiche sind hier nicht erlaubt!!) | sI:5,78,2,-5,4 |
| sF:wert,wert,wert | erzeugt Gleitkomma-Datensätze aus den angegebenen Werten, wobei die Reihenfolge der Werte wie angegeben beibehalten wird! (Zahlenbereiche sind hier nicht erlaubt!!) | sF:34.5,3.4,6,5,-43.4 |
Bereichsdefinitionen
Folgende Bereichsdefinitionen sind möglich:
| Beschreibung | Beispiel |
| Zahl | 45 |
| Zahl mit Einheitenvielfachen | 15k |
| mehrere Zahlen, durch Beistrich getrennt | 34,15k,24.4m |
| Zahlenbereich mittels Bindestrich | 3-15 |
| Ganzzahl-Bereiche | I3-15 |
| Eine bestimmte Anzahl von Werten aus einem Zahlenbereich | 13:45-130 |
| Normreihe | E12:10k-80k |
| Dezimale Reihe | D3:10-300 |
Mögliche Normreihen mit logarithmisch verteilten Werten pro Dekade: E3,E6,E12,E24,E48
Mögliche dezimale Reihen mit gleicheverteilten Werten pro Dekade: D2, D4, D10, D20, D40
Mögliche Einheitenvielfache: m,u,n,p,f,a,k,M,G,T
Einheiten
- Als Einheit kann jede gültige SI Einheit angegeben werden
- Beginnt die Einheit mit einem Gleichheitszeichen, so wird die Einheit bei der Darstellung der Variable in der angegebenen Form und mit dem angegebenen Prefix erzwungen.
- Als Sondereinheiten sind zulässig
| dB | Dezibel |
| % | Prozent |
| ppm | parts per million |
| ° | Grad |
| € | Euro |
| $ | Dollar |
- Bei komplexen Zahlen kann durch Beistrich getrennt die Darstellung der komplexen Zahl definiert werden. Folgende Darstellungsvarianten sind zulässig:
| karti | karthesische Darstellung mit "i" als komplexen Operator (1+2i) |
| kartj | karthesische Darstellung mit "j" als komplexen Operator (1+2j) |
| poldeg | Polarkoordinaten Darstellung in Grad 2arg30° |
| polrad | Polarkoordinaten Darstellung in Radianten 2arg0.2 |
| polideg | Exponentialdarstellung mit "i" als komplexen Operator und Winkel in Grad 1*e^20°i |
| poljrad | Exponentialdarstellung mit "i" als komplexen Operator und Winkel in Radiant 1*e^0.2i |
| poljdeg | Exponentialdarstellung mit "i" als komplexen Operator und Winkel in Grad 1*e^20°j |
| poljrad | Exponentialdarstellung mit "i" als komplexen Operator und Winkel in Radiant 1*e^0.2j |